Thermodynamic bound on the asymmetry of cross-correlations
News 2023/08/23
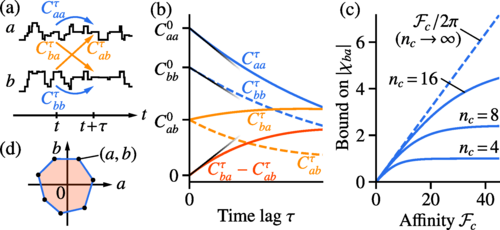
The principle of microscopic reversibility says that, in equilibrium, two-time cross-correlations are symmetric under the exchange of observables. Thus, the asymmetry of cross-correlations is a fundamental, measurable, and often-used statistical signature of deviation from equilibrium. Here we find a simple and universal inequality that bounds the magnitude of asymmetry by the cycle affinity, i.e., the strength of thermodynamic driving. Our result applies to a large class of systems and all state observables, and it suggests a fundamental thermodynamic cost for various nonequilibrium functions quantified by the asymmetry. It also provides a powerful tool to infer affinity from measured cross-correlations, in a different and complementary way to the thermodynamic uncertainty relations. As an application, we prove a thermodynamic bound on the coherence of noisy oscillations, which was previously conjectured by Barato and Seifert. We also derive a thermodynamic bound on directed information flow in a biochemical signal transduction model.
See below for more information.