物性理論
| 研究室 | 研究者紹介 | 研究テーマ |
|---|---|---|
| 小形研究室 | 小形 正男 教授 | 超伝導と強相関電子系 |
| 常行研究室 | 常行 真司 教授 | 第一原理に基づく物質構造予測と電子状態理論 |
| 藤堂研究室 | 藤堂 眞治 教授 | 計算物理、強相関多体系、乱れた系の統計物理 |
| 桂研究室 | 桂 法称 准教授 | 量子多体系の基礎理論、磁性、トポロジカル物性 |
| 樺島研究室 | 樺島 祥介 教授 | 統計力学と情報科学の境界領域の研究 |
| 辻研究室 | 辻 直人 准教授 | 物性理論、非平衡量子多体系 |
| 蘆田研究室 | 蘆田 祐人 准教授 | 量子多体物理と量子光学の境界領域における理論的研究 |
物性物理学では、巨視的な自由度からなる系の性質を微視的な原理から理解する ことを目的にしている。
微視的な原理というのは、量子力学、統計力学を中心と して、電磁気学、光学、古典力学などを物質間の基礎的な相互作用を支配する物 理法則である。
相対性理論は素粒子や宇宙を記述するときよく現れるが、固体の 電子構造や物性に電子を取り扱う場合にも重要な役割をする。
多くの自由度が織りなす協力現象は、様々な対称性の変化を伴う相転移はじめ自然を理解する上で極めて重要である。
巨視的な物理系を扱う物性物理学の対象は、固体に限らず、超流体という量子液体も含む液体や、最近ではレーザー冷却された原子におけるボース・アインシュタイン凝縮も守備範囲になるなど、扱う領域は広い。
実際、Powers of Tenという本(P. Morrison, Scientific American Books) を見ると、この世界を、超銀河団から始まり、どんどん十倍づつ拡大して見てゆき、 クォークに至る非常にスケールが異なる現象を紹介しているが、その中核をなす十数ページを舞台としているのが物性物理学である。
最近の物性物理学の目標は、新しいタイプの物性現象の発見、予言、解明である。
そこ では、既存や新合成された物質の性質を説明するだけでなく、このようにすれば 新物性が出るのでないかといった積極的な提案もされ「物質設計」と呼ばれている。
また、複雑な集団運動を記述する非線形方程式の解明や、量子力学の特徴 を活かしたミクロな量子ダイナミックスについても研究が進められている。
本物理学教室の物性理論分野には、
- 小形正男研究室
- 常行真司研究室
- 藤堂眞治研究室
- 桂 法称研究室
- 樺島祥介研究室
- 辻 直人研究室
- 蘆田祐人研究室
という7研究室があり、上で述べた物性物理学の様々な分野をカバーして精力的な研究が行われている。
その特徴は、 (a) 非常に基本的な物性基礎論から、現実の物質に即した物質科学に亘る幅広いスペクトルをもった理論グループであること、 (b) 多くの科学研究費や21世紀COEなどを通じて、理論家と実験家が密接に交流していることであろう。
以下に、各研究室を簡単に紹介する。
【小形研究室】
物性理論つまり、固体や液体など多くの粒子が相互作用している状態を、ミクロな理論によって理解しようとしている。とくに量子現象が顕著に現れる、電子やスピンの問題を中心に研究 している。
教科書に出てくる問題は簡単な場合で、相互作用を考えていない 理想気体とか、自由電子ガスについて書かれている。しかし、現実には金属中で電子は1Åくらいの平均間隔で存在しているので、クーロン斥力の効果を無視するわけにはいかないはずである。 それにも関わらず、金属中では電子はサラサラ流れているようにも見える。 もちろん、ドロドロになって電子が流れているような物質も存在する。 さらに超伝導になることもしばしばある。
このように、ドロドロぐちゃぐちゃになっている状態は、自由ガスというよりは 液体状態である。このような状態を、電子同士の強いクーロン斥力 を考慮して理論的に理解しようというのが、われわれの1つの大きなテーマである。 すべての理解への道は険しく遠いが、できる範囲のところで少しずつ研究を 積み重ねているつもりである。 具体的には、高温超伝導を含む新しい超伝導物質の問題や、金属が絶縁体に相転移する現象の理解、 磁性の発現やその種々の状態、磁性と伝導電子の相互作用などを考え、何か 今まで誰も思いつかなかったような現象を見出そうと日々努力している。
(a) 高温超伝導:すでに発見から20年ほど経ってしまっているが、未だに 新たな発見があり続けていて、興味が尽きない。
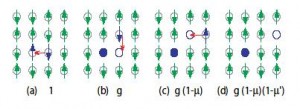
高温超伝導は、絶縁体に動けるキャリアを少し導入することによって発現する ので、超伝導と絶縁体との関係は最も興味ある研究の1つである。 これを理解するために、金属絶縁体転移と超伝導の関係を調べている。 電子の密度が適当な値のときに、クーロン斥力を強くしていくと、 気体液体転移のような1次相転移としての 金属絶縁体転移が実現すると考えられている。 この様子を実空間で理解するために、上の図のような状態を考えて、これらが 波動関数中でどのような重みを持っているかというようなことを考えている。 このようにしてできた絶縁体状態にキャリアを導入すると、高温超伝導が実現するといえる。
(b) コバルト酸化物の超伝導:
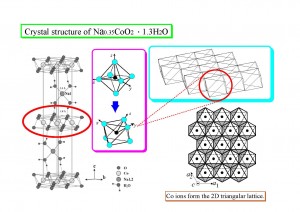
この図は、コバルトを含む酸化物の結晶の図である。正八面体の中央の 黒丸がコバルト原子であり、周りの水色の丸は酸素を表している。 この正八面体の構造が層状構造を組んで、右下の図のような2次元三角格子を形成している。 このような結晶構造を眺めながら、モデルハミルトニアンを構成しミクロな 理論を考えるのである。
コバルトを含む酸化物は2003年に日本で発見された比較的新しい超伝導体 である。この物質は、上の図にあるように、正八面体が非常にきれいな2次元 三角格子を組んでいるので、理論的に大変興味が持たれている。 高温超伝導体が2次元正方格子上で実現していることとの対比を通して、 どのような相違点や共通点が超伝導に重要であるかなどが 明らかになると期待されるからである。
われわれのグループでは、この新しい物質に対しても、いろいろな角度から 超伝導の可能性をミクロに研究している。 最終的には実験との比較によって、どのような理論が適当であるのか 決まるのであるが、理論として(トッピなアイデアを含めて)可能な 超伝導メカニズムを考えることは、とても楽しいことである。
(c) 有機伝導体:
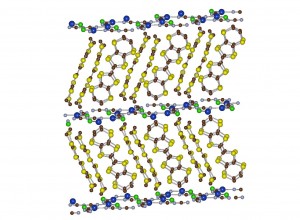
この図は有機伝導体の1つである。中央の黄色い平面状の分子が重なっていて、 上の方から見ると2次元平面を作っている。この分子の上を電子が移動することに よって、やはり2次元電子系が実現している。青い原子分子の部分は、電子などの 供給源ではあるが、2次元面を隔てる役割もしている。
この一見複雑な構造からわかるように、 分子の修飾などいろいろと微妙な変更が可能である。このことによって、 有機物質の構造には、ほぼ無限大の可能性があるといえる。 有機物質は物性の宝庫である。
このような有機伝導体においても、超伝導や金属絶縁体転移などが 様々なバージョンとして現れる。これらも理論的に比較的単純なモデルによって 理解することが進められている。 たとえば、新しい秩序状態である「電荷秩序状態」という概念が、最近の有機物の研究で 明らかになった。 この新しい秩序状態近傍での電荷の自由度に着目し、それの引き起こす 特異な現象やダイナミクス、および超伝導に関する研究も行なっている。
さらに例えば、幾何学的フラストレーションによる量子融解とか、電荷秩序近傍の 電荷ゆらぎによって引き起こされる超伝導とか、スピン自由度の特異なふるまい、 局在スピンとの相互作用をもつ1次元有機系、といったことも調べている。
【常行研究室】
原子論・電子論にもとづくコンピュータシミュレーション手法、 分子動力学法や第一原理電子状態計算を使って、できる限り具体的な物質の物性を探ることにより、 物性物理学の新たな展開を目指している。とくに固体表面や超高圧下など,実験だけでは十分な情報が得られない極限条件での物質の振る舞いを明らかにすること,またそのための新しいシミュレーション手法開発が,常行研究室の主要なテーマである。
(1) 表面科学
半導体や金属表面への分子吸着,表面化学反応,触媒反応,これらは応用にも直結する重要な現象であるが,現在の実験観測手法では空間分解能,時間分解能の両面で情報不足である。そこで実験結果に依存しない非経験的な計算機シミュレーション(第一原理計算)を使って,表面吸着分子の安定構造,その電子状態,化学反応経路の理論探査などを行っている。
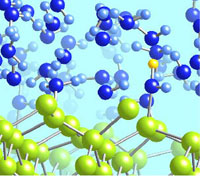
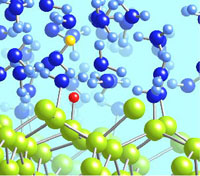
複数の分子間でプロトンを「リレー」しながらシリコン表面に水分子が
解離吸着(H2O+2Si→H-Si + HO-Si)する様子。(始状態と終状態)
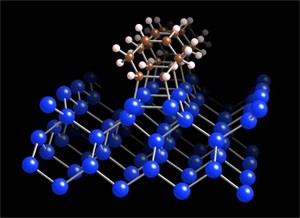
Si表面に吸着したシクロヘキサジエンの構造(理論予測)
(2) 高圧物性
固体水素の構造相転移と金属化,YH3(金属水素化物)の絶縁体金属転移など,実物実験が困難だったり,たとえ出来たとしても情報量の極めて少ない超高圧下で,物質がどのような結晶構造をとるか,またどのような電子相転移があり得るかを,第一原理計算や拡張アンサンブル法を使って探っている。
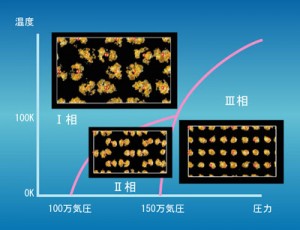
固体水素の相図と経路積分法(第一原理)で見た分子性固体水素の構造。
(3) 水素を含む固体
実験的観測が困難な固体中の水素原子分布や電子状態を,第一原理的手法(第一原理分子動力学法,経路積分法)を用いて調べている。とくに原子核が軽いことによる量子効果に着目した研究を行い,量子効果がむしろ原子の局在化をもたらす可能性(量子局在化現象)を指摘している。
(4) 新しい電子状態計算手法の開発
オーソドックスな密度汎関数理論に基づく第一原理電子状態計算手法の開発に加え,波動関数理論の立場で電子相関を取り入れた固体の電子状態計算を行う新しい手法「トランスコリレイティッド法」や,拡張アンサンブルを用いた構造探査法の開発を行っている。
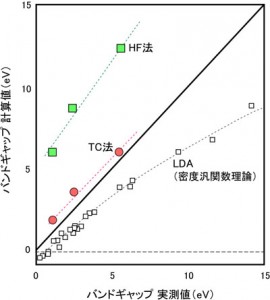 トランスコリレイティッド(TC)法により計算された様々な半導体の
トランスコリレイティッド(TC)法により計算された様々な半導体の
バンドギャップとその実測値。同じ波動関数理論である
ハートリーフォック(HF)法から大幅な改善が見られる。